In some application domains it is not enough to build reliable software systems, one wants proved-correct software.
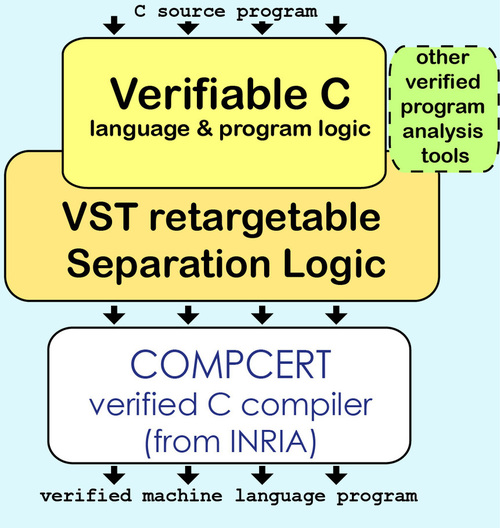
Andrew W. Appel’s lab at Princeton appears to be working on something that could be both instructive and directly useful for developing FAI: The Verified Software Toolchain Project.
It assures with machine-checked proofs that the assertions claimed at the top of their toolchain really hold in the machine-language program, running in the operating-system context.
Formally verifying all the layers of a program stack in Coq is an impressive mathematical and practical engineering feat. And a valuable tool in and of itself for anyone wanting to run code that absolutely must operate correctly.
But I also want to understand more about how the Coq proof techniques they employ work. Relational decomposition, separation logics, paramodulation, and other styles of proofs they use all look like valuable techniques for getting the kinds of guarantees we might eventually want in an FAI.
See on vst.cs.princeton.edu