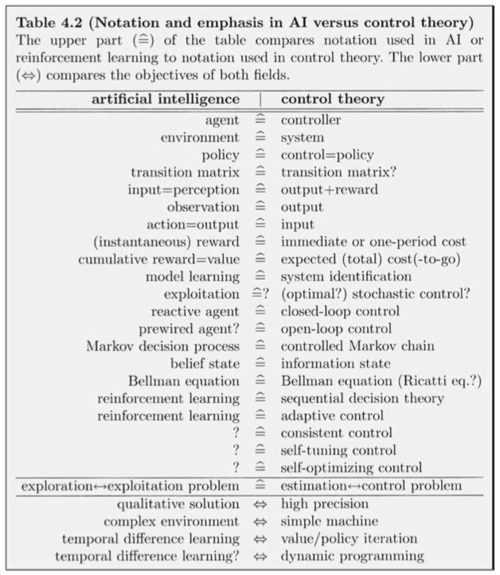
Specified as control theory, FAI is an ultra-high frequency, stable, low-sensitivity, high-response, robust, closed-loop, non-linear, self-optimizing controller with no overshoot, which performs a flawlessly reliable error-free policy of beneficial transitions that amplify (or at least preserve) humane values over time. It can be shown that many of these design specifications are in tension, but that trade-offs can possibly be explored more profitably when construed as control theory.

I’ve been thinking about this for around a year now, but I’m not a control theory expert. If you know control theory and have an interest in FAI, I’m curious what you think of the following questions:

1) Which criteria in this description are in conflict?

2) What are the typical design trade-offs that occur in real controller design for these dilemmas?

3) Of the conflicting FAI requirements, which of the constraints are most important? And design wise, which are the cheapest to provide?

4) What do analogues of theorems like the Routh-Hurwitz Stability Criterion mean in the context of AI design?

5) What do “observability” requirements imply about the need for sensor density? If FAI design requirements eventually need to exert optimal control over fine-grained physical processes, will they necessarily require sensors at that granularity as well? It seems like control theory and physics requires this.

6) Having a controller actively optimize physics at error tolerances lower than your sensors’ distinguishing ability seems to not be possible. What can be said about “non-active” methods? Those don’t seem hopeful, but are there escape hatches? It seems like the most likely possibility is something like “non-verified” actions, where you assume you cause positive utility without checking. How hopeful are these approaches?

7) How critical a penalty is the “loss of gain” required for closed loop feedback? How much does this undermine the ability to achieve low sensitivity to initial conditions? G(s) seems to quickly diminish. That might make it difficult to have FAI’s outcome not be highly sensitive to initial conditions (e.g., the state of the world at takeoff), which seems undesirable. Also, the rate of stable increases for intelligence might be limited by these “loss of gain” functions (i.e. Gs / (1+ Gs)). These limits don’t appear to be fatal for hard takeoff plausibility, but they do place upper-bounds on the rate of take-off for systems with the required sensitivity to be friendly. This points towards an uncomfortable conclusion that you can formally prove FAI can’t takeoff as fast as certain classes of pathologically designed UFAI (e.g. Malicious AI). This observation does seem to go beyond the normal observation that “destruction is easier than construction” and may show a lower-bound on the size of the gap between these two cases.

8) Attempting to specify FAI as control theory connotes that the controller and the plant can both be modeled without much loss as having a state space which is a Cartesian product of a fixed number of known continuous variables. This is probably false for FAI. In FAI, after a certain point, there can be no conceptual distinction between “controller” variables and “plant” variables, and the state space is more like a space of programs than like R^n or 2^n for some n. Is this correct? And if so, does it make control theory a poor tool to analyze FAI design in?